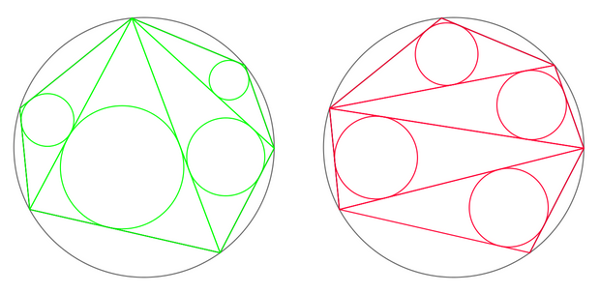
Choose any number of points on a circle and connect them to form a polygon.

This polygon can be carved into triangles in any number of ways by connecting its vertices.

No matter how this is done, the sum of the radii of the triangles’ inscribed circles is constant.

This is an example of a Sangaku (literally, “mathematical tablet”), a class of geometry theorems that were originally written on wooden tablets and hung as offerings on Buddhist temples and Shinto shrines during Japan’s Edo period (1603-1867). This one dates from about 1800.