A curiosity attributed to a Professor E. Ducci in the 1930s:

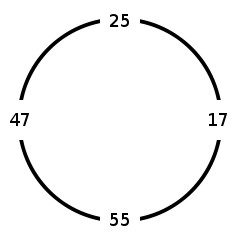
Arrange four nonnegative integers in a circle, as above. Now construct further “cyclic quadruples” of integers by subtracting consecutive pairs, always subtracting the smaller number from the larger. So the quadruple above would produce 22, 8, 38, 8, then 14, 30, 30, 14, and so on.

Ducci found that eventually four equal numbers will occur.

A proof appears in Ross Honsberger’s Ingenuity in Mathematics (1970).