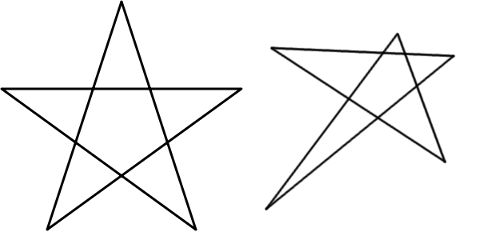
A puzzle by A. Korshkov, from the Russian science magazine Kvant:
It’s easy to show that the five acute angles in the points of a regular star, like the one at left, total 180°.
Can you show that the sum of these angles in an irregular star, like the one at right, is also 180°?
|
SelectClick for Answer |
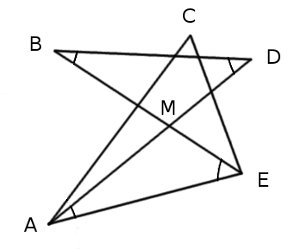
Join two of the star’s adjacent vertices, such as A and E. Triangles BMD and AME have an angle in common (the congruent angles at M), so the sum of angles B and D in triangle BMD equals the sum of angles A and E in triangle AME. This means that the sum of the star’s five angles equals the sum of the angles of triangle ACE — which is 180°.
|


