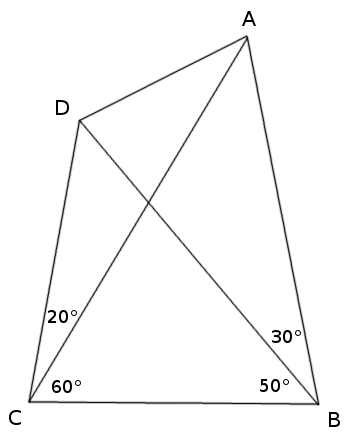
I just ran across this in an old Math Horizons article — Andy Liu, vice president of the International Mathematics Tournament of the Towns, calls it “one all-time favorite geometric gem.” Given the four angles shown, compute angle CAD. “It sounds like a trivial exercise at first, and therein lies its charm.”
Liu doesn’t give the solution, but he does give a hint — I’ll put that in a spoiler box in case you want to work on the problem first.
|
SelectClick for Answer |
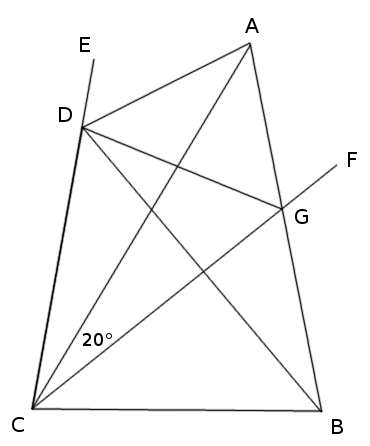
Extend CD to E and draw CF so that angle ACF is 20 degrees. Let CF cut AB at G and join DG. He says that’s the construction we need, but the only other clue he gives is to look for excenters.
After some squinting, I think A may be the excenter of triangle GCD, since CA bisects angle GCD. This could be confirmed by showing that DA bisects angle EDG and GA bisects angle FGD. I don’t quite have time to follow this out, but it looks promising, and in keeping with the theme of Liu’s article, cited below. (Forgive my inexpert drawing.)
(Andy Liu, “A Better Angle From Outside,” Math Horizons 5:2 [November 1997], 27-29.)
|


