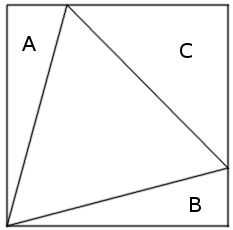
If an equilateral triangle is inscribed in, and has a common vertex with, a rectangle, as shown above, then areas A + B = C.

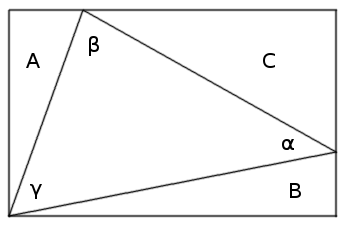
If a triangle with angles α, β, γ is inscribed in, and has a common vertex with, a rectangle, as shown below, and if the right triangles opposite α, β, γ have areas A, B, C, respectively, then A cot α + B cot β = C cot γ.

Somewhat related: A Curious Equality.

(Tom M. Apostol and Mamikon Mnatsakanian, “Triangles in Rectangles,” Math Horizons 5:3 [February 1998], 29-31.)