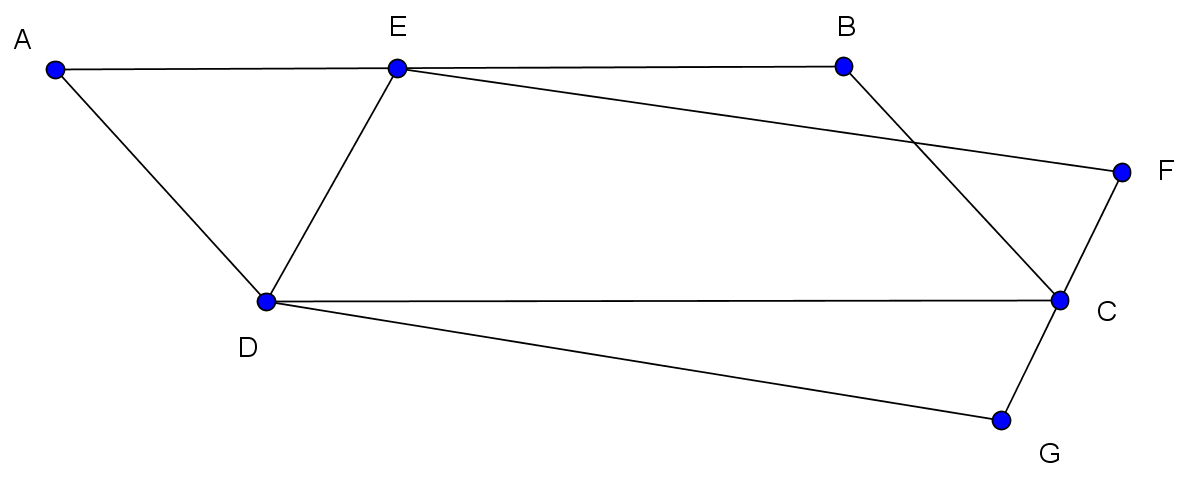
Point E lies on segment AB, and point C lies on segment FG. The area of parallelogram ABCD is 20 square units. What’s the area of parallelogram EFGD?
|
SelectClick for Answer |
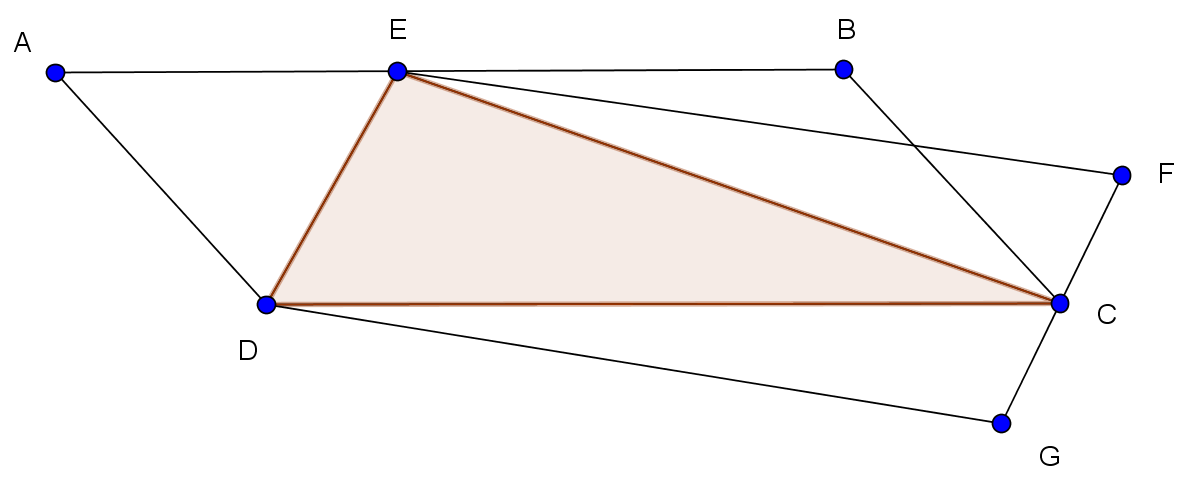
Draw EC. Now parallelogram ABCD and triangle EDC share a common base (DC), and they have the same altitude (a perpendicular from E to DC). So triangle EDC has half the area of parallelogram ABCD.
But likewise, parallelogram EFGD and triangle EDC share a common base (ED), and they have the same altitude (a perpendicular from C to ED). So triangle EDC has half the area of parallelogram EFGD.
Since both parallelograms have twice the area of the same triangle, their own areas must be equal. So the area of EFGD is 20 square units.
(From Alfred S. Posamentier, Math Wonders to Inspire Teachers and Students, 2003.)
|

