
Death Valley contains an enormous jagged salt flat produced by the evaporation of an ancient lake.
It takes its name from a 1934 National Park Service guidebook, which declares that “only the devil could play golf on such rough links.”

Death Valley contains an enormous jagged salt flat produced by the evaporation of an ancient lake.
It takes its name from a 1934 National Park Service guidebook, which declares that “only the devil could play golf on such rough links.”
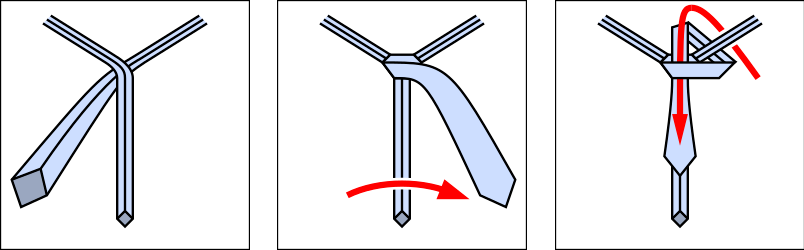
In 1999, while serving as research fellows at Cambridge University’s Cavendish Laboratory, physicists Thomas Fink and Yong Mao made a mathematical study of necktie knots. They published a summary in Nature that year and a detailed exposition in Physica A in 2000.
They found that, if knots are modeled as persistent random walks on a triangular lattice, there are exactly 85 ways to tie a tie. Of the 10 knots they scored as most aesthetic (for symmetry and balance), only four (four-in-hand, Pratt knot, half-Windsor, Windsor) are well known to Western men; interestingly, the simplest of the remainder, the unassuming small knot, above, is popular in the communist youth organization in China.

The squares of a 9×9 board are colored as shown, and then its surface is covered with 40 dominoes. Each domino covers two orthogonally adjacent squares, and the uncovered square is a black square on the boundary.
A move shifts a domino along its length by one square, so that it covers one empty square and exposes another. Prove that, for each of the black squares on the board, there’s a sequence of moves that will uncover it.
The programming language SIMPLE “was designed to make it impossible to write code with errors in it.”
The language has only three commands, STOP, BEGIN, and END. “No matter how you arrange the statements, you can’t make a syntax error.”
The name stands for Sheer Idiots Monopurpose Programming Linguistic Environment.

The creature from the Black Lagoon has the best possible pedigree. As director Jack Arnold was planning the iconic monster’s 1954 debut, his eye fell on his Academy Award nomination certificate for With These Hands, a documentary he’d worked on three years earlier.
“I said, ‘If we put a gilled head on [the Oscar statuette], plus fins and scales, that would look pretty much like the kind of creature we’re trying to get,'” he told Cinefantastique in 1975. “So they made a mold out of rubber, and gradually the costume took shape.”
Former Disney animator Milicent Patrick and makeup artist Bud Westmore collaborated on the creature. “They gave him some human characteristics, which helped to make him sympathetic,” Arnold said. Today the film is regarded as a classic of monster horror — but it didn’t earn an Oscar.

We have more respect for a man who robs boldly on the highway, than for a fellow who jumps out of a ditch, and knocks you down behind your back. Courage is a quality so necessary for maintaining virtue, that it is always respected, even when it is associated with vice.
— James Boswell, Life of Samuel Johnson, 1791
Andrzej Bartz offered these “doubly true” alphametics in the May 2017 issue of Word Ways. If the letters in each equation encode digits, what mathematical facts do these expressions represent?
CCCLVI + CCCI + CCLI = CMVIII
ONE + THIRTYNINE + NINETYONE = THREE + NINE + THIRTY + EIGHTYNINE
TWO × TWO + TEN × FIVE = SIX × NINE
The story goes that one day when Cézanne was picknicking in the country with some friends and a collector, the latter suddenly realized that he had dropped his overcoat somewhere on the way. Cézanne raked the landscape with his gaze, then exclaimed: ‘I’ll swear that black over there doesn’t belong to nature!’ Sure enough, it was the overcoat.
— André Malraux, The Voices of Silence, 1978
1931 saw the publication of a remarkable detective novel. The Floating Admiral had been written by 12 members of the Detection Club, London’s society of mystery writers:
They had written a chapter apiece, serially, without communicating. Each inherited the manuscript from the last and had to make some private sense of the story, including their own complications, before passing it on to the next contributor. To ensure fair play, each writer had to supply a satisfactory solution to the snowballing mystery when they turned in their own chapter.
Amazingly, it worked. Jacques Barzun wrote, “These members of the (London) Detection Club collaborate with skill in a piece of detection rather more tight-knit than one had a right to expect. There is enough to amuse and to stimulate detection; and the Introduction by Dorothy Sayers and supplements by critics and solvers give an insight into the writers’ thoughts and modes of work.”

On April 8, 1959, when keepers arrived at the Spectacle Reef lighthouse in Lake Huron to prepare it for a new season, they discovered a note:
To Whom It May Concern:
At 1705 hours my plane went down 400 kilometers out at 035 to 050 degrees. I was one mile northeast of here at 5000 feet when my engine went quite dead. I tried to make it in but landed in the water. At that time there were large open areas of water. I did not try to land on the ice as it did not look thick enough. Also I wanted to get as close to this light as possible.
The plane went down in about two minutes after it landed. Before it did it floated close enough to a floe for me to jump. The ice was not over two inches thick. Another large body of water separated me from the light so I waited.
Suddenly the wind shifted to the northeast. The ice I was on started to move. At the very last moment one quarter of the ice ground against the ice packed around the light. My ice floe broke up fast so I ran for the light. I got ashore but was wet from falling in. My clothes froze before I could get the door open.
Once inside I used your towels and overshoes to keep from freezing.
About 2100 I got your stove lit. I hooked up the batteries and lit your warning lamp. The radio receiver worked but the transmitter was dead. I didn’t know enough about it to make it work. I have used the batteries until they are going dead. I sat up last night sending out SOS calls by blinking the main light.
Right now I am deliberating whether to stay here or cross the ice. From the chart I will have eleven miles to travel. There are large water holes, thin ice which had been broken into pieces by the wind yesterday. There is hardly any wind today. We have had two freezing nights, so I ought to make it in about four hours. I want to go now because it is nice weather.
Also I did not file a flight plan so no one will look for me another two or three days. The weather may be bad again.
I have made a mess of your building. I hope you will forgive me. I am going to take some equipment with me, binoculars, coat, hat, blankets, etc. I will turn them into the United States Coast Guard as soon as I get ashore.
Signed,
M.Sgt. William J. Wyman
USAF
The note bore no date. Wyman had departed Saginaw in a Piper Super Cruiser on Feb. 22, headed for the former Kinross Air Force Base near Sault Ste. Marie. He had never arrived. No trace of him was ever found.
(Thanks, Charles.)