Opaque Sets

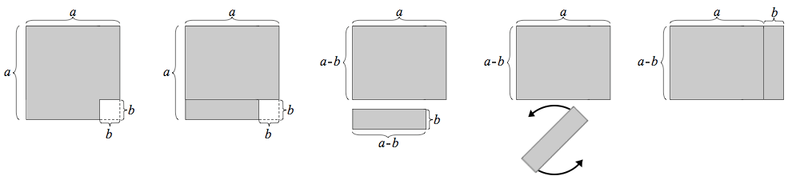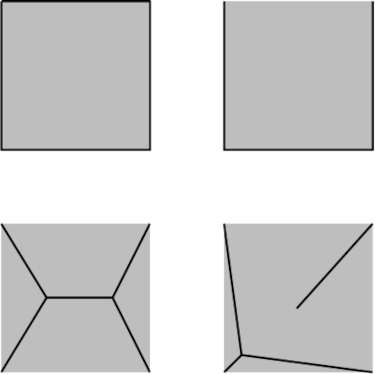
https://commons.wikimedia.org/wiki/File:Unit_Square_Opaque_Forest_Solutions.svg

A creature living in the plane can’t see through a unit square — the square’s four line segments block its line of sight from any angle. Is there a way to achieve the same result using fewer building materials? Removing one of the square’s sides does the job — this requires only 3 units of line segment and still prevents anyone from seeing across the square’s area. The arrangement at lower left does better still, requiring only about 2.732 units. And the one at lower right requires only about 2.639 units.

Is that the shortest possible opaque set for the square? Possibly — but no one has been able to prove it.

| Science & Math

Misc

  • Samuel Johnson said that sending a timid boy to a public school is “forcing an owl upon day.”
  • Inscribed over the door of the library at Murcia, Spain: “Here the dead open the eyes of the living.”
  • TRICE in Pig Latin is ICE TRAY.
  • 35 × 1482 × 9760 = 3514829760 (Jean-Marc Falcoz)
  • “Mauve is pink trying to be purple.” — Whistler

Pekwachnamaykoskwaskwaypinwanik Lake is a lake in Manitoba. Its name is Cree for “where the wild trout are caught by fishing with hooks.”

Muckanaghederdauhaulia, a townland in County Galway, means “pig-marsh between two sea inlets.”

Saaranpaskantamasaari, an island in northeastern Finland, means “an island shat by Saara.”

Mamungkukumpurangkuntjunya is a hill in South Australia. Its name means “where the devil urinates.”

(Thanks, Colin.)

| Language · Literature · Quotations · Science & Math

An Unanswered Question

One of the most beautiful and moving of the bird-songs heard throughout the country which [French merchant Nicolas] Denys governed [in 17th-century Acadia], is that of the Veery, or Wilson’s Thrush. The Maliseet Indians of the Saint John River, as Mr. Tappan Adney has recently told us, say this bird is calling Ta-né-li-ain′, Ni-kó-la Dĕn′-i Dĕn′-i?, that is, ‘Where are you going, Nicolas Denys?’ and Mr. Adney thinks this an actual echo from the days of our author.

— From William Francis Ganong’s 1908 introduction to Denys’ Description and Natural History of the Coasts of North America, 1672

| History · Science & Math

Coverup

https://commons.wikimedia.org/wiki/File:Moser_worm_problem.svg
Image: Wikimedia Commons

Suppose you have a publicity-seeking inchworm and want to keep him to yourself. What’s the smallest cover you can contrive to keep him hidden? He can writhe into any shape that an inch-long creature can take; you must always be able to turn your shape to keep him covered.

Strangely, we don’t yet know the answer to this question. Mathematician Leo Moser first posed it in 1966, and various proposals have driven the upper bound as low as π/12 ≈ 0.2618, but we still don’t know whether smaller covers are possible. It’s known as Moser’s worm problem.

| Science & Math

Early Adopter

At the start of H.G. Wells’ 1895 novella The Time Machine, the Time Traveller explains to his friends that “any real body must have extension in four directions: it must have Length, Breadth, Thickness, and — Duration.” This idea, of conceiving time as a fourth dimension, had been broached in the 18th century, but it had first been treated seriously in a mysterious letter to Nature in 1885:

“I [propose] to consider Time as a fourth dimension of our existence. … Since this fourth dimension cannot be introduced into space, as commonly understood, we require a new kind of space for its existence, which we may call time-space.”

The letter writer identified himself only as “S.” Was this Wells? Apparently not: In his 1934 Experiment in Autobiography Wells wrote, “In the universe in which my brain was living in 1879 there was no nonsense about time being space or anything of that sort. There were three dimensions, up and down, fore and aft and right and left, and I never heard of a fourth dimension until 1884 or there-about. Then I thought it was a witticism.”

So someone had anticipated Wells’ idea by a full decade. As far as I know, his identity has never been discovered.

(Via Paul J. Nahin, Holy Sci-Fi!, 2014.)

| Literature · Science & Math

Round and Square

This rank impossibility by Kokichi Sugihara won second prize in the Neural Correlate Society’s 2016 illusion of the year contest.

The key is that the top of each cylinder is not a planar curve. Dickinson College mathematician David Richeson has created an interactive applet that you can use to examine the shape, and see his paper below for an explanation of the math and the template of a paper model.

(David Richeson, “Do the Math!: Sugihara’s Impossible Cylinder,” Math Horizons 24:1 [September 2016], 18-19.)

| Oddities · Science & Math

Reciprocity Redux

sallows reciprocity post

From Lee Sallows:

“The above three strips of ten numbers have an intriguing property. They record how many times each of the decimal digits (shown at left) occur in the other two strips. Hence the 6 in the left-hand strip identifies the number of 0’s in strips B and C, while the 2 in the centre strip counts the number of 3’s present in strips A and C. Moreover, the same property holds for every number in all three strips.”

See Reciprocation.

(Thanks, Lee.)

| Science & Math