Another puzzle from Henry Ernest Dudeney, The Canterbury Puzzles, 1908:
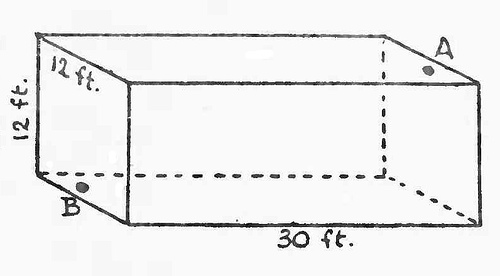
“Inside a rectangular room, measuring 30 feet in length and 12 feet in width and height, a spider is at a point on the middle of one of the end walls, 1 foot from the ceiling, as at A, and a fly is on the opposite wall, 1 foot from the floor in the centre, as shown at B. What is the shortest distance that the spider must crawl in order to reach the fly, which remains stationary? Of course the spider never drops or uses its web, but crawls fairly.”
|
SelectClick for Answer |
“Though this problem was much discussed in the Daily Mail from 18th January to 7th February, 1905, when it appeared to create great public interest, it was actually first propounded by me in the Weekly Dispatch of 14th June, 1903.
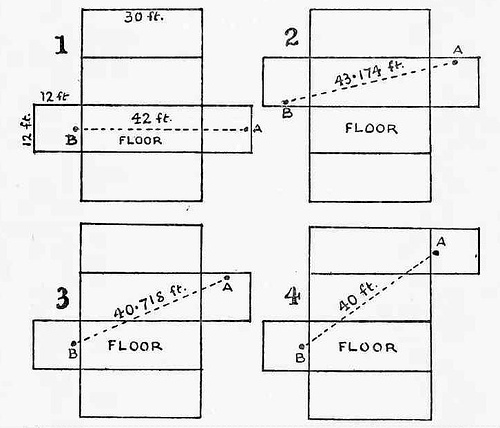
“Imagine the room to be a cardboard box. Then the box may be cut in various different ways so that the cardboard may be laid flat on the table. I show four of these ways and indicate in every case the relative positions of the spider and the fly and the straightened course which the spider must take, without going off the cardboard. These are the four most favourable cases, and it will be found that the shortest route is in No. 4, for it is only 40 feet in length (add the square of 32 to the square of 24 and extract the square root). It will be seen that the spider actually passes along five of the six sides of the room! Having marked the route, fold the box up (removing the side the spider does not use), and the appearance of the shortest course is rather surprising. If the spider had taken what most persons will consider the obviously shortest route (that shown in No. 1), he would have gone 42 feet! Route No. 2 is 43.174 feet in length and route No. 3 is 40.718 feet. I will leave the reader to discover which are the shortest routes when the spider and fly are 2, 3, 4, 5, and 6 feet from the ceiling and floor respectively.”
|


