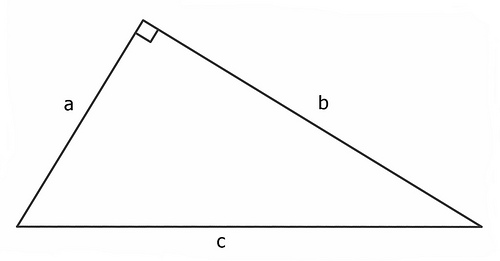
We’re told that, in any right triangle, a² + b² = c². But consider:

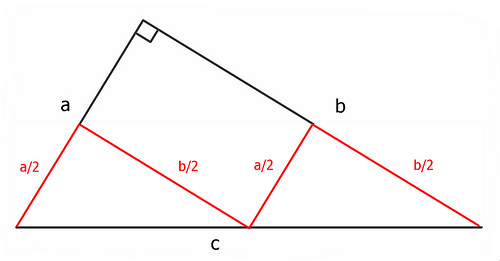
In the figure above, the total length of the red line is 2(a/2) + 2(b/2), or a + b. And again:

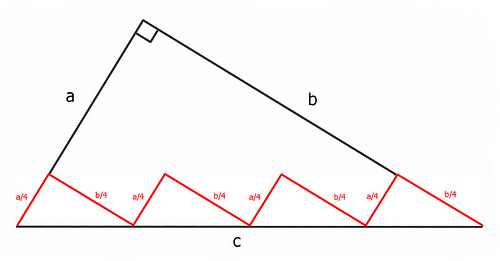
Here the red line’s length is 4(a/4) + 4(b/4), which is still a + b.

With each iteration, the red line more closely approximates c, but its length remains a + b. At the limit, then, it seems, a + b = c. Was Pythagoras mistaken?