From Henry Dudeney:
A better class of puzzle is the well-known one of the Railway. If New York and San Francisco are just seven days’ journey apart, and if trains start from both ends every day at noon, how many trains coming in an opposite direction will a train leaving New York meet before it arrives at its destination at San Francisco?
|
SelectClick for Answer |
Solution to Track Meet:
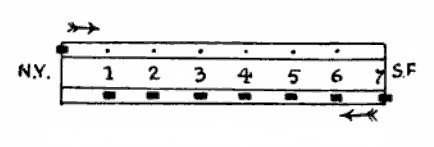
This puzzle, which many people find so perplexing, is quite easy if you refer to the diagram I have given. It will be seen that at the moment the train starts from New York there are six trains already on the way in the positions indicated, since it is a seven days’ journey. The train numbered 7 also starts at the same time. Therefore the train has to meet all these seven. But when the New York train is at point 1, an eighth train will be leaving San Francisco, when it is at point 2 a ninth train will be leaving, at point 3 a tenth, at point 4 an eleventh, at point 5 a twelfth, and at point 6 a thirteenth train will be leaving San Francisco. Therefore the train will meet thirteen others on the journey. Of course, at the moment of its arrival a train will be just starting, but it cannot be said to ‘meet’ this one on the journey.
UPDATE: An insightful reader points out that New York and San Francisco are in different time zones. This means that at the instant we start, the intermediate trains won’t precisely occupy the numbered positions in Dudeney’s diagram — they’ll be offset a bit. And that changes the answer to 14! In effect, the “train that will be just starting” will be fairly out of the station when we arrive (if only just) and thus counts as an extra encounter. That’s my best interpretation, anyway, in viewing Dudeney’s puzzle in this new light.
|

