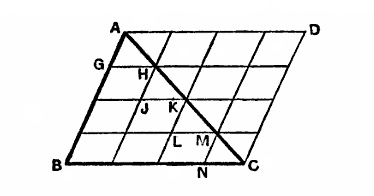
Here’s proof that one leg of a triangle always equals the sum of the other two.

ABC is our triangle. Extend it make a parallelogram, as shown, and divide the parallelogram into a grid. Obviously,

AB + BC = (AG + HJ + KL + MN) + (GH + JK + LM + NC).

Now let the grid grow increasingly fine: Instead of dividing the parallelogram into a 4×4 grid, make it 5×5, then 6×6, and so on. With each iteration, the stairstep figure described above will approximate AC more closely, and yet its total length will always equal AB + BC. Thus, at the limit, AB + BC = AC. Where is the error?

(From Henry Dudeney’s Canterbury Puzzles, via W.W. Rouse Ball’s Mathematical Recreations and Essays, 1892.)