This problem dates from at least 1774; this version appeared in the American Mathematical Monthly of December 1902:
Three Dutchmen and their wives went to market to buy hogs. The names of the men were Hans, Klaus, and Hendricks, and of the women, Gertrude, Anna, and Katrine; but it was not known which was the wife of each man. They each bought as many hogs as each man or woman paid shillings for each hog, and each man spent three guineas more than his wife. Hendricks bought 23 hogs more than Gertrude, and Klaus bought 11 more than Katrine. What was the name of each man’s wife?
(There are 21 shillings in a guinea.)
|
SelectClick for Answer |
The American Mathematical Monthly‘s published solution to Husbands and Wives:
Let x represent the number of one of the women’s hogs, and y the number of her husband’s; then by the conditions of the problem y2 = x2 + 63. Consequently x2 + 63 must be an integer, since 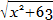 represents the number of hogs. The equation y2 – x2 = 63 or (y + x) (y – x) = 63 admits of three solutions, viz., 63 × 1, 21 × 3, and 9 × 7:
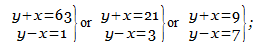
whence y = 32, x = 31; y = 12, x = 9; y = 8, x = 1. Since 32 = 9 + 23 and 12 = 1 + 11, 32 belongs to Hendricks, 12 to Klaus, 9 belongs to Katrine, 1 to Gertrude.
Therefore 32 Hendricks, 31 Anna; 12 Klaus, 9 Katrine; 8 Hans, 1 Gertrude.
Hence, Hendricks is Anna’s husband, Klaus is Katrine’s husband, and Hans is Gertrude’s husband.
The numbers here are correct, but the names are confused. Correct are:
Hendricks 32
Gertrude 9
Klaus 12
Katrine 1
Hans 8
Anna 31
So Hendricks is married to Anna, Klaus to Gertrude, and Hans to Katrine. (Thanks, Shrey.)
|
