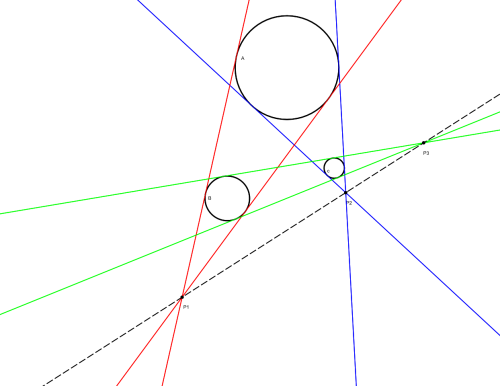
Draw three nonintersecting circles of different sizes, and bracket each pair of them with tangents. Each pair of tangents will intersect in a point, and these three points will always lie along a line.
On being shown this theorem, Cornell engineering professor John Edson Sweet paused and said, “Yes, that is perfectly self-evident.” What intuitive proof had he seen?
|
SelectClick for Answer |
Sweet imagined the diagram in three dimensions. He thought of the circles as spheres, and each pair of tangents (red, blue, and green) as a cone enfolding two of the spheres. The three spheres sit on one plane, and we can imagine lowering another plane on top of them. The two planes will always intersect in a line, and as each cone is tangent to both planes, the apex of each cone will always lie on this line.
03/08/2012 UPDATE: Peter Winkler, in Mathematical Mind-Benders, notes that the second plane may not exist — imagine, for example, a small sphere directly between two larger spheres.
But Winkler points out that Nathan Bowler of Trinity College, Cambridge, has found another solution that appeals to three dimensions: Imagine that each of the three spheres is wearing a “hat” — a cone with a 90-degree apex. Each pair of apices determines a line that passes through an intersection of circle tangents, and the three apices also determine a plane that intersects the first plane in a line, as before.
|

