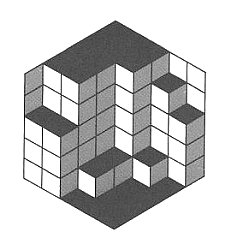
A calisson is a flat French candy traditionally manufactured in the shape of two equilateral triangles joined along an edge. Suppose a quantity of these are packed randomly into a hexagonal container:
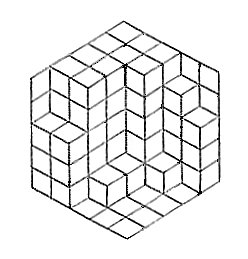
Each candy must take one of three orientations: east-west, northeast-southwest, or northwest-southeast.
As it happens, no matter how the candies are packed into the hexagon, an equal number will take each of these three orientations.
In the May 1989 issue of the American Mathematical Monthly, Guy David and Carlos Tomei demonstrated this with a beautifully intuitive “proof without words.” What had they seen?