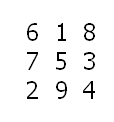
The lowly 3×3 magic square has modest pretensions — each row, column, and diagonal produces the same sum.
But perhaps it’s magicker than we suppose:
6182 + 7532 + 2942 = 8162 + 3572 + 4922 (rows)
6722 + 1592 + 8342 = 2762 + 9512 + 4382 (columns)
6542 + 1322 + 8792 = 4562 + 2312 + 9782 (diagonals)
6392 + 1742 + 8522 = 9362 + 4712 + 2582 (counter-diagonals)
6542 + 7982 + 2132 = 4562 + 8972 + 3122 (diagonals)
6932 + 7142 + 2582 = 3962 + 4172 + 8522 (counter-diagonals)
(R. Holmes, “The Magic Magic Square,” The Mathematical Gazette, December 1970)
More: Any of the equations above will still hold if you remove the middle digit or any two corresponding digits in each of the six addends.
Yet more: (6 × 1 × 8) + (7 × 5 × 3) + (2 × 9 × 4) = (6 × 7 × 2) + (1 × 5 × 9) + (8 × 3 × 4)
I think everything above will work for any rotation or reflection of the square (that is, for any normal 3×3 magic square). I haven’t checked, though.
