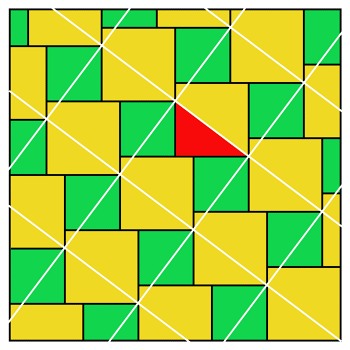
This tiling pattern is sometimes referred to as Pythagorean because it can be construed to prove the Pythagorean theorem.

The red area is a right triangle. The square of its shorter side is equivalent to a green square, and the square of its longer side is equivalent to a yellow square.

One green and one yellow square can be cut up and reassembled to fit into one of the canted white squares, which is equivalent to the square of the red triangle’s hypotenuse. Hence a² + b² = c².