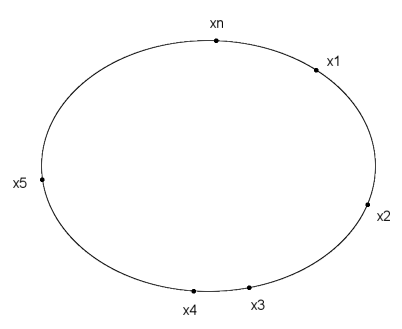
A problem by Hungarian mathematician Laszlo Lovász:
A track has n arbitrarily spaced fuel depots. Each depot contains a quantity of gasoline; the total amount of gas is exactly enough to take us around the track once. Prove that, no matter how the gas is distributed, there will be a depot at which an empty car can fill up, proceed around the track picking up gas at each depot, and complete a full round trip back to its starting depot.
|
SelectClick for Answer |
Imagine taking a practice run in a car that has plenty of gas. Along the way the car will pick up exactly enough gas to take it once around the track, so it will complete the practice run with the same amount of fuel that it started with. If we keep an eye on the car’s fuel gauge, we’ll find that it reaches its lowest point as we arrive at one of the depots (call it xi). Any additional gas in our tank at that point is unneeded; we know it will never be used. Now if we start at xi with an empty tank we know we’ll have enough gas to get from each depot to the next, running out of gas just as we arrive back at xi.
|

