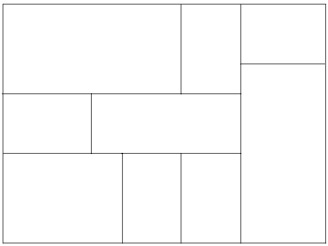
A large rectangle is partitioned into smaller rectangles, each of which has either integer height or integer width (or both). Prove that the large rectangle itself must have integer height or integer width.
|
SelectClick for Answer |

Place the rectangle’s lower left corner at the origin of a checkerboard grid each of whose squares has side 0.5. Now, because each of the smaller rectangles has at least one integer side, each will be colored half white and half black. Consequently the large rectangle itself must be half white and half black.
Now suppose that the large rectangle does not have integer width. What heights will permit it to contain equal areas of black and white? Only those with precisely an even number of checkerboard rows — the integers.
From Stan Wagon, “Fourteen Proofs of a Result about Tiling a Rectangle,” American Mathematical Monthly, Vol. 94 (1987), pp. 601-617, via Peter Winkler, Mathematical Puzzles: A Connoisseur’s Collection (2004).
|

