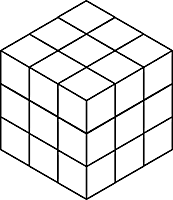
We have 27 wooden cubes. The first is marked A on every face, the second B, and so on through the alphabet to Z. The 27th cube is blank. Is it possible to assemble these cubes into a 3×3×3 cube with the blank cube at the center, arranging them so that cube A adjoins cube B, cube B adjoins cube C, and so on, forming a connected orthogonal path through the alphabet?
|
SelectClick for Answer |
No, it’s not possible. Imagine painting the large cube with a checkerboard pattern. As we move through the alphabet we’ll change colors at each step; if we’re to succeed there must be 13 red cubes and 13 black ones (omitting the center cube). But the surface of a large checkerboard cube contains 12 cubes of one color and 14 of the other. So it can’t be done.
|

