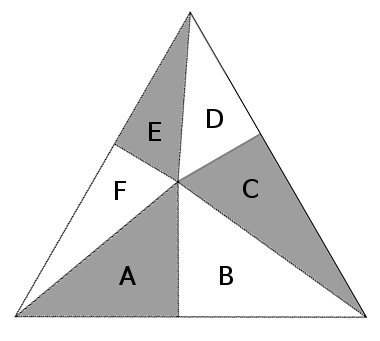
Choose an arbitrary point inside an equilateral triangle and draw segments to the vertices and perpendiculars to the sides. This divides the triangle into six smaller triangles, A, B, C, D, E, and F. Prove that the areas A + C + E and B + D + F are equal.
|
SelectClick for Answer |
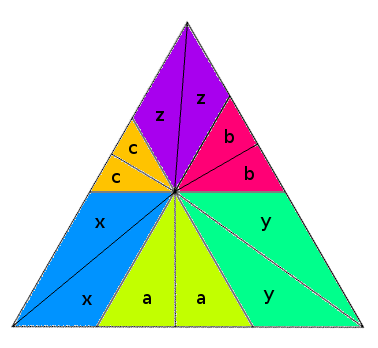
Draw three additional lines through the chosen point, each parallel to a side of the large triangle. This divides it into three parallelograms and three equilateral triangles. The parallelograms are bisected by their diagonals and the triangles by their altitudes, so A + C + E = x + a + y + b + z + c = B + D + F.
From Quantum, January 1990, via Ross Honsberger, Mathematical Chestnuts From Around the World, 2001.
|


