Prove that if each point in the plane is colored red, yellow, or blue, a unit segment must exist whose endpoints are the same color.
|
SelectClick for Answer |
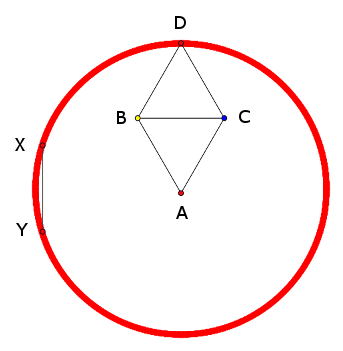
Set up two abutting equilateral triangles ABC and BCD with unit sides, as above, and suppose A is red. In order to avoid a unit segment with similarly colored endpoints, D must also be red. By the same reasoning, every point at this distance from A must also be red. But this describes a monochromatic circle, and we can always find two points on this circle that are 1 unit apart. Thus it’s impossible to avoid having a unit segment with ends of the same color.
From Joseph Konhauser, Macalester College, St. Paul., Minn., in the Pi Mu Epsilon Journal, 1984, 668, via Ross Honsberger, Mathematical Chestnuts From Around the World, 2001.
|