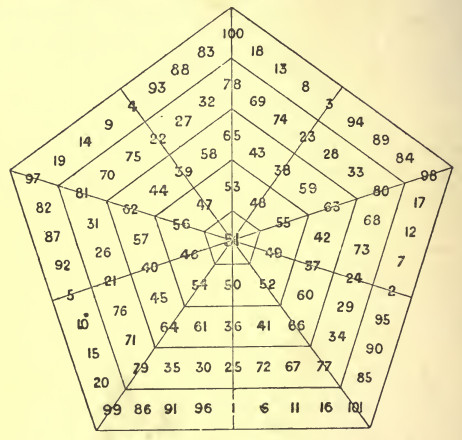
From Edward Falkener’s Games Ancient and Oriental and How to Play Them (1892), a magic pentagon. “It will be observed that the five sides of each pentagon are all equal, and that the five diameters, from one angle to the centre of the opposite side, are each 459, which is nine times the central number 51, which is also the mean number, the series being 1-101. And, further, that the inner pentagon is 510, or 10 times the mean number; the next pentagon 1,020, or 20 times the mean; the next 1,530, or 30 times the mean; and the outside pentagon 2,040, or 40 times the mean.” Evidently this was devised by Mikhail Frolov for Les carrés magiques (1886). (08/25/2015 Reader MJ has perfected this further, making each side of the outermost ring total 459, the same as the diagonals.)

From the Gentleman’s Magazine, October 1768, a “magic circle of circles” by Benjamin Franklin:

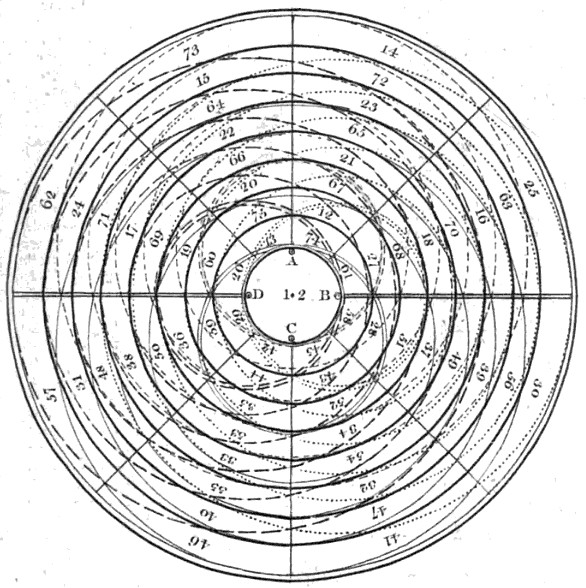
The numbers run from 12 to 75. Each ring and each radius, added to the central number 12, gives 360, the number of degrees in a circle. The dashed lines define four additional sets of circles, with centers at A, B, C, and D, each with five rings; each ring, when added to 12, also gives the total 360. (The 12 is added arbitrarily to bring the total to 360; remove it and the whole arrangement remains magic.)

From the inimitable R.V. Heath:

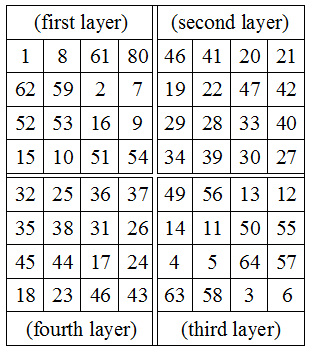
This 8×8 magic square can be cut into four smaller magic squares. When these four are stacked in the order indicated they produce a pandiagonal magic cube, each of whose rows, columns, and diagonals produces the total 130. Also: “The original eighth-order magic square has the additional property that if either set of alternate rows and either set of alternate columns be deleted — and this can be done in four ways — the remaining 16 numbers form a fourth-order magic square of magic constant 130.” (From Howard Whitley Eves, Mathematical Circles Squared, 1972.)

(Thanks, Ray.)