Lori has an icky problem: Worms keep crawling onto her bed. She knows that worms can’t swim, so she puts each leg of the bed into a pail of water, but now the worms crawl up the walls of the room and drop onto her bed from the ceiling. She suspends a large canopy over the bed, but worms drop from the ceiling onto the canopy, creep over its edge to the underside, crawl over the bed, and drop.
Desperate, Lori installs a water-filled gutter around the perimeter of the canopy, but the worms drop from the ceiling onto the outer edge of the gutter, then crawl beneath. (The worms are very determined.) What can Lori do?
|
SelectClick for Answer |
She’s on the right track. Lori can stop the worms by installing a gutter around the canopy’s perimeter, but one that extends inward, under its lip, rather than outward:
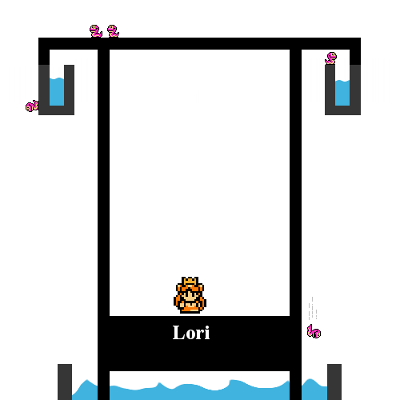
Now a worm that drops from the ceiling onto the canopy and creeps beneath will pass under this gutter and find itself surrounded by a moat, of sorts, that prevents it from reaching the underside of the canopy.
From MIT’s Balint Virag, via Dartmouth mathematician Peter Winkler’s excellent Mathematical Mind-Benders (2007). Winkler adds, “If the worms have no higher-up way to get in her bedroom, Lori can more easily accomplish this same task by encircling the room itself with a water-filled gutter.”
|

