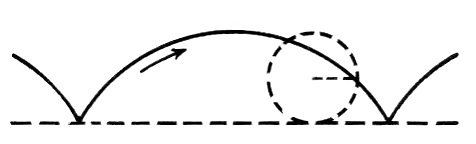
As a circle rolls along a line, a point on its circumference traces an arch called a cycloid. The arch encloses an area three times that of the circle, a result commonly proven using calculus. Now Armenian mathematician Mamikon Mnatsakanian has devised a “sweeping-tangent theorem” that accomplishes the same proof using intuition:

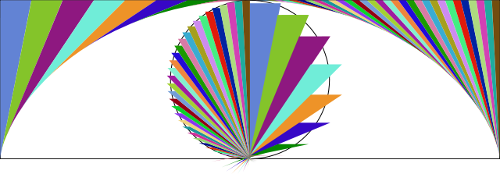
Imagine a tangent to the rolling circle. As the circle rolls, the tangent sweeps out a series of vectors (approximated here using colors). If these vectors are then gathered to a common point while preserving their length and orientation, they form a sort of bouquet whose size and shape turn out to match exactly those of the original circle. Because the enclosing rectangle has four times the area of the rolling circle (2πr × 2r = 4πr²), this shows that the area under the arch has three times the circle’s area.

All this is proven rigorously in Mnatsakanian’s 2012 book New Horizons in Geometry, written with his Caltech colleague Tom Apostol. The two have now collaborated on some 30 papers showing that many surprising and useful results that heretofore had required integration can now be obtained using intuitive methods that can appeal even to a young student.

That’s a welcome outcome for Mnatsakanian, who found himself stranded in the United States when the Armenian government collapsed in 1990. Apostol writes, “When young Mamikon showed his method to Soviet mathematicians they dismissed it out of hand and said ‘It can’t be right. You can’t solve calculus problems that easily.'”