Utica College mathematician Hossein Behforooz devised this “permutation-free” magic square in 2007:

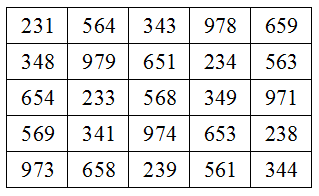
Each row, column, and long diagonal totals 2775, and this remains true if the digits within all 25 cells are permuted in the same way — for example, if we exchange the first two digits of each number, changing 231 to 321, etc., the square retains its magic sum of 2775. Further:

231 + 659 + 973 + 344 + 568 = 2775
979 + 234 + 653 + 341 + 568 = 2775
231 + 343 + 568 + 654 + 979 = 2775
564 + 979 + 233 + 348 + 651 = 2775
231 + 654 + 563 + 978 + 349 = 2775
231 + 348 + 654 + 979 + 563 = 2775

And these combinations of cells maintain their magic totals when their contents are permuted in the same way.

(Hossein Behforooz, “Mirror Magic Squares From Latin Squares,” Mathematical Gazette, July 2007.)