We’ve mentioned before that you can estimate π by dropping needles on the floor. (Reader Steven Karp also directed me to this remarkable solution, from Daniel A. Klain and Gian-Carlo Rota’s Introduction to Geometric Probability [1997].)

Here’s a related curiosity. If a circle of diameter L is placed at random on a pattern of circles of unit diameter, which are arranged hexagonally with centers C apart, then the probability that the placed circle will fall entirely inside one of the fixed circles is

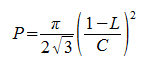
If we put k = C/(1 – L), we get

And a frequency estimate of P will give us an estimate of π.

Remarkably, in 1933 A.L. Clarke actually tried this. In Scripta Mathematica, N.T. Gridgeman writes:

His circle was a ball-bearing, and his scissel a steel plate. Contacts between the falling ball and the plate were electrically transformed into earphone clicks, which virtually eliminated doubtful hits. With student help, a thousand man-hours went into the accumulation of N = 250,000. The k was about 8/5, and the final ‘estimate’ of π was 3.143, to which was appended a physical error of ±0.005.

“This is more or less the zenith of accuracy and precision,” Gridgeman writes. “It could not be bettered by any reasonable increase in N — even if the physical error could be reduced, hundreds of millions of falls would be needed to establish a third decimal place with confidence.”

(N.T. Gridgeman, “Geometric Probability and the Number π,” Scripta Mathematica 25:3 [November 1960], 183-195.)