Three coins are lying on a table: a quarter, a half dollar, and a silver dollar. You claim one coin, I’ll claim the other two, and then we’ll toss all three. A coin that lands tails counts zero, and a coin that lands heads wins its value (in cents, 25, 50, or 100) for its owner. Whichever of us has the larger score wins all three coins. If all three coins land tails then we toss again.
Which coin should you claim to make the game fair — that is, so that each of us has an expected win of zero?
|
SelectClick for Answer |
Surprisingly, the game is fair regardless of which coin you choose. Here’s a table of the possible payoffs:
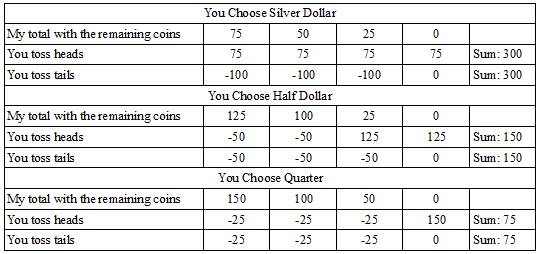
In each case the holder of the single coin wins just enough (when he does win) to lead to a zero expectation for each player.
David L. Silverman, who discovered this, found that this game is fair with any set of coins, no matter how they’re divided, provided that their values show a successive doubling (e.g., 25, 50, 100).
From Martin Gardner, “Charles Addams’ Skier and Other Problems,” in Wheels, Life and Other Mathematical Amusements, 1983.
UPDATE: The mathematical principle here is sound, but the presentation muddies it a bit. The expected outcomes are equal after a coin has been chosen, but properly speaking choosing a coin is part of the game. If both players start with nothing, as described, then choosing the silver dollar gives the best chance of winning. (Thanks, Seth and Tim.)
|

