“Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily, so that no two shall walk twice abreast.”

The Rev. Thomas Penyngton Kirkman posed this query innocently in The Lady’s and Gentleman’s Diary in 1850. It’s trickier than it looks — though seven solutions are possible, they’re difficult to discover by trial and error. Here’s one:

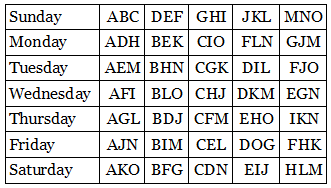
Each letter appears once in each row, but no two letters share a cell more than once. The problem’s simplicity made it popular among Victorian amateur mathematicians, and Kirkman later complained that it had eclipsed his more serious work — though he took pains to dispute James Joseph Sylvester’s claim to have invented the problem himself.

Do such problems generally have solutions? Surprisingly, the answer remained unknown until just last January, when Oxford mathematician Peter Keevash showed that the answer is yes if certain basic requirements are met. Keevash’s result was “a bit of an earthquake as far as design theory is concerned,” said Cambridge mathematician Timothy Gowers.

Now that the schoolgirl problem is under control, a related challenge has taken its place. If 20 golfers want to arrange themselves into different foursomes on five successive days, is it possible to plan the groups so that each golfer plays no more than once with any other golfer? Formally the “social golfer problem” remains unsolved — though tournament organizers work out individual solutions every day.

(Thanks, Martha.)