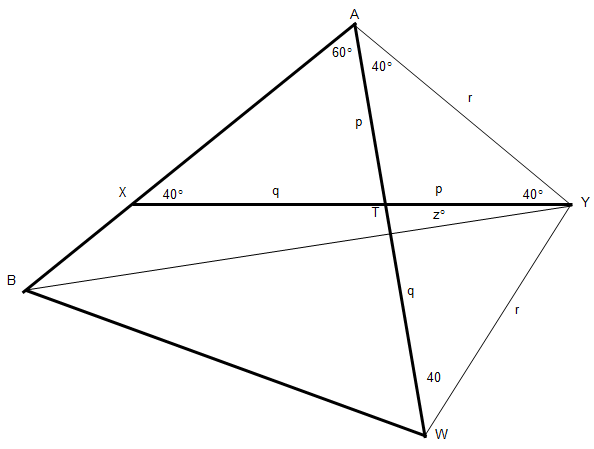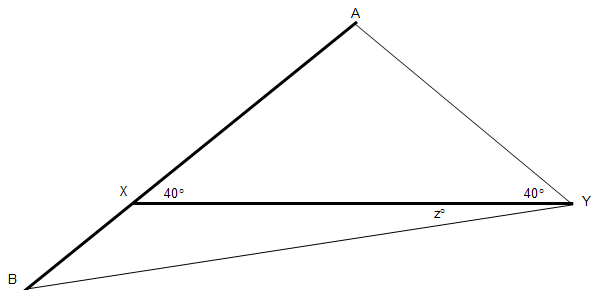
AB = XY. Find z°.
| SelectClick for Answer | |
|---|---|
Construct equilateral triangle ABW. Now: ∠WAY = 40° (because each interior angle of ABW is 60° and the interior angles of triangle XAY must total 180°) p = p (because triangle ATY is isosceles) q = q (because AB = AW = XY = p + q) ∠AWY = 40° (because triangles ATX and YTW are similar) r = r (because triangle AYW is isosceles) This shows that ABWY is a kite, a quadrilateral with two pairs of equal-length sides, each pair adjacent. The diagonals of a kite are perpendicular, so the triangle that contains angle z also contains interior angles measuring 90° and 80°. Angle z is 10°. (Thanks, Derek.)
| |