Quick Thinking

Some “ridiculous questions” from Martin Gardner:

1. A convex regular polyhedron can stand stably on any face, because its center of gravity is at the center. It’s easy to construct an irregular polyhedron that’s unstable on certain faces, so that it topples over. Is it possible to make a model of an irregular polyhedron that’s unstable on every face?

2. The center of a regular tetrahedron lies in the same plane with any two of its corner points. Is this also true of all irregular tetrahedrons?

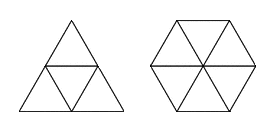
3. An equilateral triangle and a regular hexagon have perimeters of the same length. If the area of the triangle is 2 square units, what is the area of the hexagon?

	Select Click for Answer
1. No. If this were possible then a perpetual motion machine could be built — on a horizontal plane the object would be constantly moving. 2. Yes. Any three points lie in the same plane. 3. Three square units: (Martin Gardner, “Ridiculous Questions,” Math Horizons 4:2 [November 1996], 24-25.)

October 24, 2015November 1, 2015 | Puzzles · Science & Math