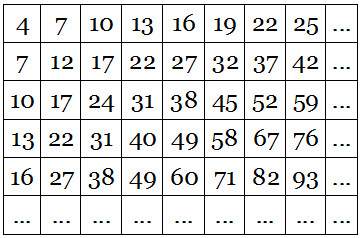
In 1934, Indian mathematician S.P. Sundaram proposed this “sieve” for finding prime numbers.

In the first row of a table, write the arithmetic progression 4, 7, 10, …, with the first term 4 and a common difference of 3.

Copy these values into the first column, and then complete each row with its own arithemetic progression, with common differences of 3, 5, 7, 9 …, in successive rows.

Now, remarkably, for any natural number N > 2, if N occurs in the table then 2N + 1 is not a prime number, and if N does not occur in the table, then 2N + 1 is a prime number. (For example, 17 appears in the table, so 35 is not prime; 23 does not appear in the table, so 47 is prime.)

(From Ross Honsberger, Ingenuity in Mathematics, 1970.)