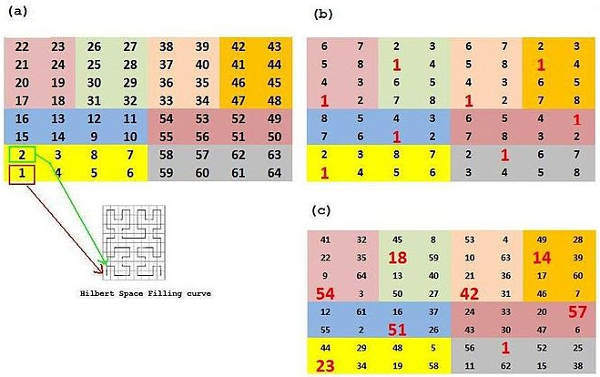
Craig Knecht, whose “terraformed” magic squares we explored in 2013, has begun to experiment with applying “magic” properties to David Hilbert’s space-filling curve.

The Hilbert curve finds its way to every cell in the square above by following the pattern shown at the lower left. Knecht divided that path into eight-cell segments, as shown in (a), and then sought solutions in which each colored eight-cell panel produced the magic sum of 260 while each of the eight ordinal positions across the eight panels did so as well. For example, in (b), a large red digit 1 marks the “first” position in each panel; the hope was to find values for these eight cells that would sum to 260, and likewise for all the “second” cells, the “third” ones, and so on.

The result, shown in (c), is a “most-perfect” magic square: Each colored panel sums to 260, and every set of cells that are 8 spaces apart on the Hilbert curve also sum to 260.

The next step was to apply this idea in three dimensions, and recently Knecht made the breakthrough shown below — a 4×4×4 “most perfect” number cube. The 64 numbers in the cube can be broken into 36 2×2 subsquares in each dimension, as shown. In all 108 of these subsquares, the four constituent numbers total 130. And as with the two-dimensional square above, a Hilbert curve can be drawn through the cube that visits each cell once, and cells that are eight cells apart on this curve sum to 260.

One of Knecht’s correspondents pointed out that the cube is even magicker than he had supposed: The “wraparound” subsquares (for example, 5, 28, 44, and 53 on the top of the cube) also sum to 130, as does each set of four corners, making a total of 192 2×2 subsquares that sum to 130.

“So in summary … making the Hilbert space-filling curve path have this magic property of values 8 spaces summing to the magic constant + this 2×2 planar criteria produces a very interesting cube!”