Cyclic Billiards - Futility Closet

A puzzle from Colin White’s Projectile Dynamics in Sport (2010): Suppose a billiard table has a length twice its width and that a rolling ball loses no energy to bounces or friction but simply caroms around the table forever. Call the angle between the launch direction and the long side of the table α. At what angle(s) should the ball be hit so that it will arrive back at the same point on the table and traveling in the same direction, so that its motion is cyclic, following the same path repeatedly?

	Select Click for Answer
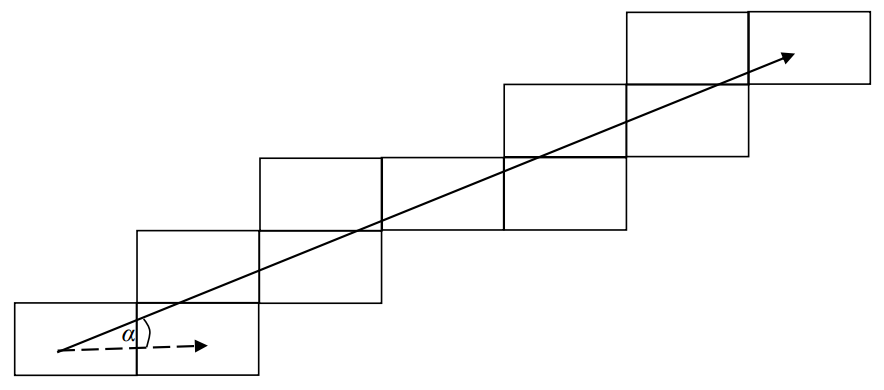
When the ball hits a cushion, it bounces back, with the angle of incidence equal to the angle of reflection. White writes, “Why not reflect the table instead?” Conceive that the ball travels in a straight line, and that each time it reaches a cushion it travels across a boundary and onto a new table. “So, we are now in a position to severely limit the allowable values of the angle, α, even if we cannot completely define those angles. The condition for cyclic motion is that the ball travels a certain number of tables up (not including the table the ball starts on), say, p tables, and so many tables to the right, say q tables. Two degenerate cases would be α = 0, in which case p = 0, and α = π/2 when q = 0. For the cases in between, 0 < α < π/2 and p > 0 and q > 0 but they must both be whole integers. In summary, we can now state that the ball will cycle on the billiard table if, and only if: i. α = 0° ii. α = π/2 = 90° iii. tan α = p/q (i.e. is a rational number) “As I stated, this is not a complete solution, but an interesting insight into a heuristic method. In justification, even if the perfect solution could be provided, it would be of no practical use to players of the game!”

Click for Answer