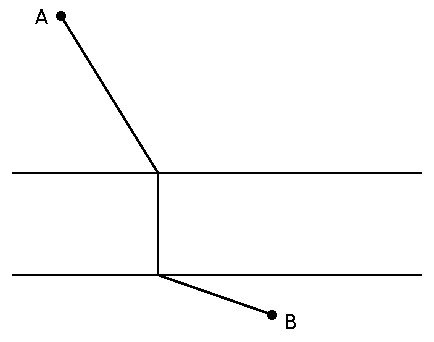
We want to build a road between two cities, A and B, that are separated by a river. We can build a bridge, but it must be perpendicular to the river’s banks, as shown. Where along the river’s length should we place the bridge if we want to minimize the total length of the road?
|
SelectClick for Answer |
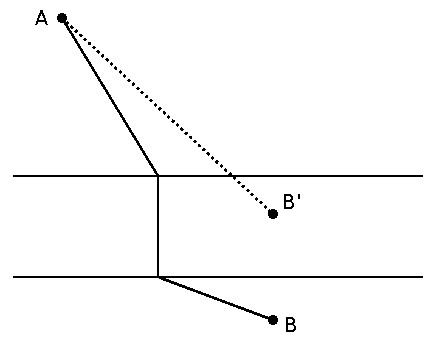
Reduce the river to a line of zero width along the bank nearest to A, and imagine moving City B up correspondingly to B’. Now a straight line drawn between A and B’ shows us where to put the bridge.
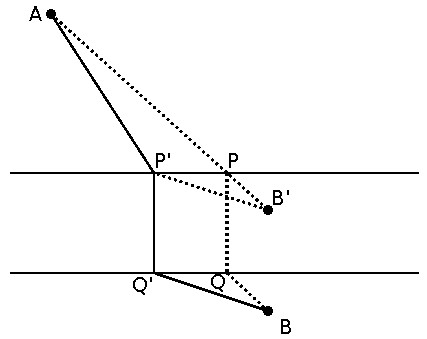
To prove this we can appeal to the triangle inequality, which says that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. In the diagram below, the optimum path we’ve suggested goes A-P-Q-B. A bridge will have the same length no matter where we build it, so let’s omit that segment from our thinking. QB is parallel to PB’, so the length of our proposed road A-P-Q-B, minus the width of the river, is equivalent to AB’.
Now consider any alternative road, say A-P’-Q’-B. Again we can ignore the width of the river, and Q’B is parallel to P’B’, so the length of the alternative road A-P’-Q’-B, minus the width of the river, is equivalent to A-P’-B’. The triangle inequality says that AB’ must be shorter than AP’ + P’B’, so A-P-Q-B must be shorter than A-P’-Q’-B. We can apply a similar argument for any other proposed site for the bridge — bridge PQ must always produce a shorter road.
From Zbigniew Michalewicz and David B. Fogel, How to Solve It: Modern Heuristics, 2000.
|



