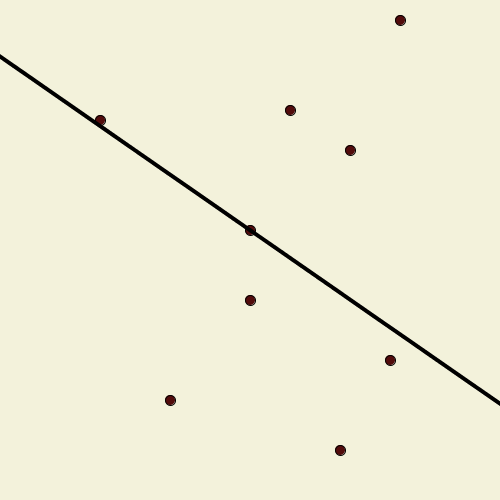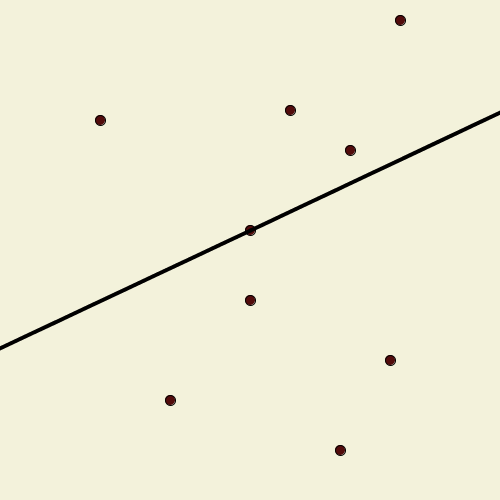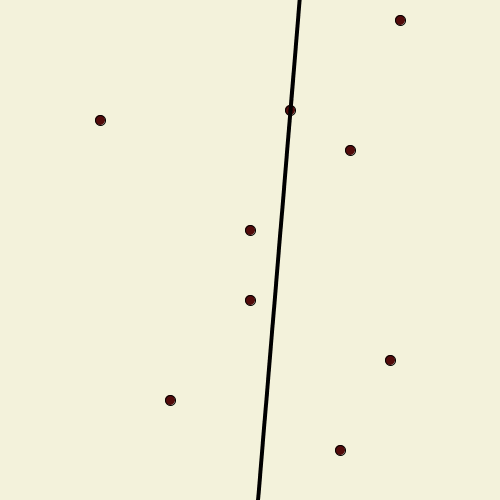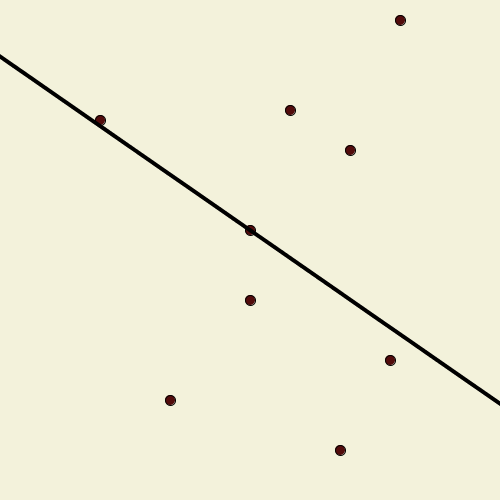
Suppose we have a finite set of points in the plane, no three of which are collinear. A line drawn through one of them pivots around that point until it encounters another point, when it adopts that point as the new pivot. Call this line a “windmill”; it continues indefinitely, always rotating in the same direction. Show that we can choose an initial point and line so that the resulting windmill uses each point as a pivot infinitely many times.
|
SelectClick for Answer |
Draw the line vertically through the centermost of the points, and color all the points to the left of it blue and all the points to the right red.
After the line has turned 180 degrees, all the points to the left of it will now be red, and those to the right will be blue. Hence every point has changed color.
Each time the pivot changes, the old pivot point returns to the same side of the line that the new one comes from. That means that the total number of blue points remains unchanged; so does the number of red points.
Since a point can change color only by serving as a pivot, this means that every point must act as a pivot at some stage. And if the line turns forever, then each point will change color infinitely many times.
This is laid out more rigorously here.
By Geoffrey Smith of the United Kingdom for the 52st International Mathematical Olympiad in Amsterdam, 2011.
The animation is from the excellent Symmetry tumblr.
|

