Charles W. Trigg offered this puzzle in the Fall 1977 issue of Pi Mu Epsilon Journal (PDF):
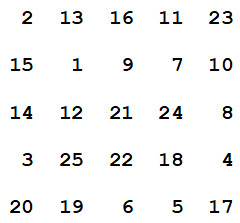
This square array contains the first 25 positive integers. Choose five, no two from the same row or column, so that the largest of the five elements is as small as possible, and justify your choice.
|
SelectClick for Answer |
Sidney Penner of Bronx Community College of CUNY, found the solution: 1, 3, 6, 8, 11. In the array, crossing out all the numbers higher than 11 eliminates all the numbers in the third row except 8. Choosing 8 means we have to forswear every other number in the fifth column, which leaves only one possibility in the fourth row, 3. And choosing 3 eliminates every other candidate in the first column, so the only available entry in the first row is 11.
At the request of problem editor Leon Bankoff, Jeanette Bickley ran the following BASIC program on a DEC PDP 11/70 computer, and it confirms Penner’s solution:

|


