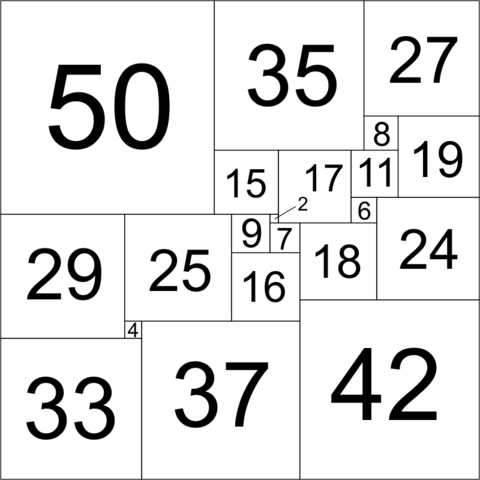
“Squaring the square” refers to tiling a square with other squares, each with sides of integer length.

In a “perfect” squared square, like the one above, each smaller square is of a different size. The Cambridge University team that first sought perfect squares found a novel way to go about it — they transformed the square tiling into an electrical circuit in which each square is a resistor that connects to its neighbors above and below, and then applied Kirchhoff’s circuit laws to that circuit.

The example below isn’t perfect, but the technique did succeed — the smallest perfect square they found is 69 units on a side.

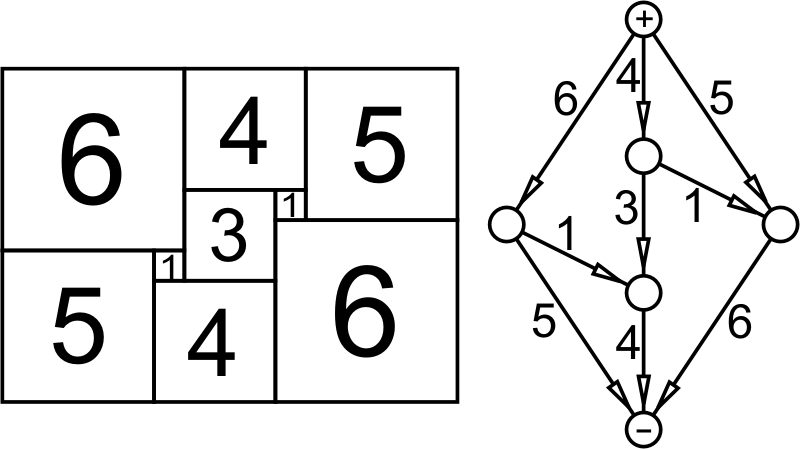
(Rowland Leonard Brooks, et al., “The Dissection of Rectangles into Squares,” Duke Mathematical Journal 7:1 [1940], 312-340.)