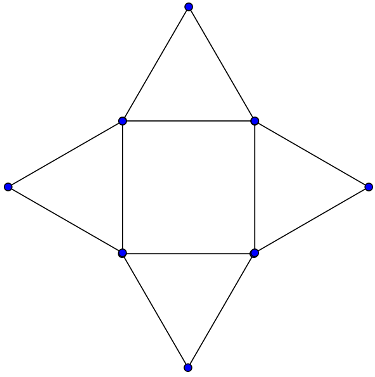
Cambridge mathematician Hallard T. Croft once asked whether it was possible to have a finite set of points in the plane with the property that the perpendicular bisector of any pair of them passes through at least two other points in the set.

In 1972 Leroy M. Kelly of Michigan State University offered the elegant solution above, a square with an equilateral triangle erected outward on each side (it also works if the triangles are erected inward).

“Croft is a great problemist,” Kelley said later. “He keeps putting out lists of problems and he keeps including that one. He’s trying to get the mathematical community to get a better example — one with more points in it. … Eight is the smallest number; and whether it’s the largest number is another question.”

So far as I know Croft’s question is still unanswered.