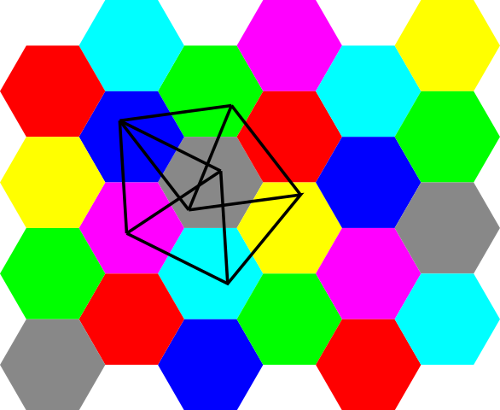
Suppose we want to paint the plane so that no two points of the same color are a unit distance apart. What’s the smallest number of colors we need?

Surprisingly, no one knows. In the figure above, the hexagons are regular and have diameters slightly less than 1. Painting them as shown demonstrates that we can do the job successfully with seven colors.

Can we do it with fewer? In 1961 brothers William and Leo Moser showed that it’s impossible with three colors: They devised a graph (the “Moser spindle,” overlaid on the hexagons above) each of whose edges has length 1. The vertices of the spindle can’t be colored with three colors without both ends of some edge having the same color.

So we don’t need more than seven colors, but we need at least four. But whether the minimum needed is 4, 5, 6, or 7 remains unknown.

04/13/2018 UPDATE: By an amazing coincidence, there’s just been some progress on this. (Thanks, Jeff.)