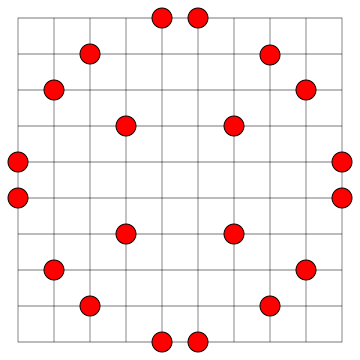
In 1917 Henry Dudeney asked: What’s the maximum number of lattice points that can be placed on an n × n grid so that no three points are collinear?

The answer can’t be more than 2n, since if we place one point more than this, we’re forced to put three into the same row or column. (The 10 × 10 grid above contains 20 points.)

For a grid of each size up to 52 × 52, it’s possible to place 2n points without making a triple. For larger grids it’s conjectured that fewer than 2n points are possible, but today, more than a century after Dudeney posed the question, a final answer has yet to be found.