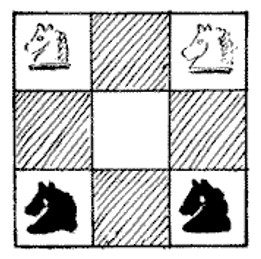
Paulo Guarini di Forli offered this puzzle in 1512. On this tiny 3 × 3 board, which is the smallest number of moves in which the white knights can exchange places with the black ones?
|
SelectClick for Answer |
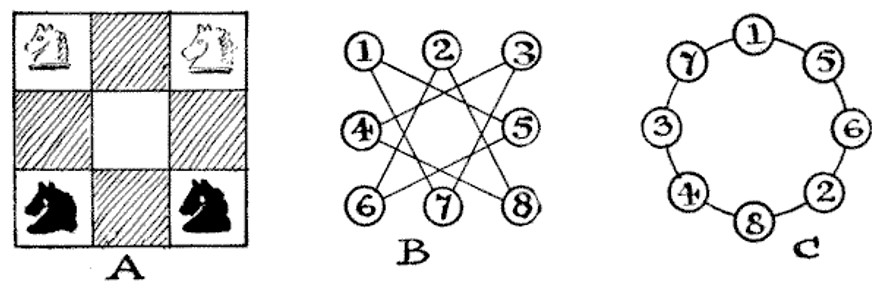
Henry Dudeney presented this solution in his 1917 Amusements in Mathematics; it’s now known as the “method of buttons and strings.” No knight will ever visit the center square, so we can ignore that; regard each of the remaining squares as a button and connect it by a string to each square that’s a knight’s move away. That produces diagram B. Now if we untangle the strings we get diagram C, a unique cycle that any knight must follow in making its way around this board.
The four knights must follow this cycle, and no two knights may ever occupy the same square. The white knights start on squares 1 and 3, the black on 6 and 8. So to exchange the white and black knights, we must advance all four knights four steps along the circle, either clockwise or counterclockwise. Since the four knights make four moves each, the task is done in 16 moves. That’s the minimum. (Somewhat paradoxically, if three white knights oppose three black ones in the starting position, the minimum number of moves drops to 8.)
|

