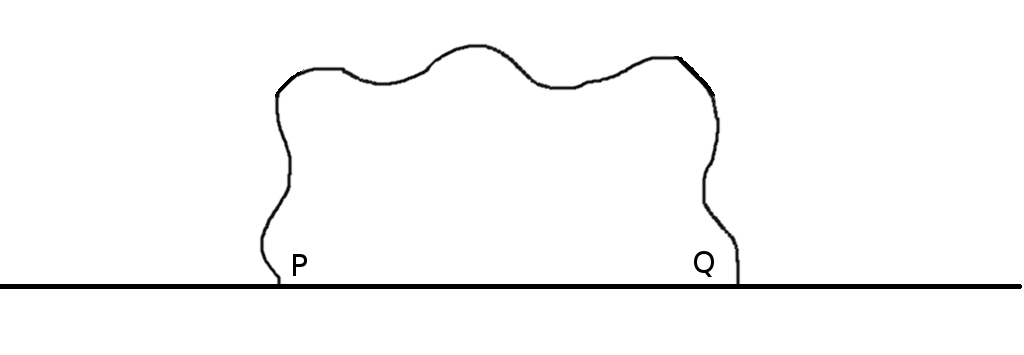
University of Illinois mathematician John Wetzel called this one of his favorite problems in geometry. Call a plane arc special if it has length 1 and lies on one side of the line through its end points. Prove that any special arc can be contained in an isosceles right triangle of hypotenuse 1.
|
SelectClick for Answer |
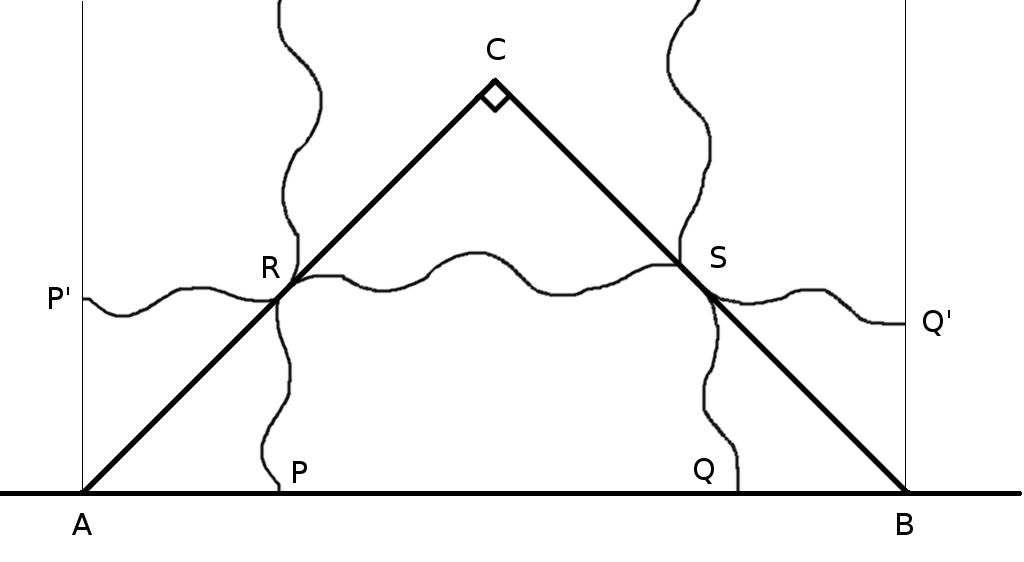
For special arc PQ, construct the smallest isosceles right triangle ABC with hypotenuse AB on line PQ that contains the arc. Let arc PQ touch the legs of this triangle at R and S. Now reflect arc PR in AC and arc SQ in BC, obtaining arcs RP’ and SQ’. Now arc PRSQ equals arc P’RSQ’ in length and lies between lines AP’ and BQ’, which are distance AB apart. The arc length is 1, and it’s not less than AB, which proves the theorem. “Wetzel concludes, ‘Pause and reflect!'”
(From Clayton W. Dodge, “Reflections of a Problems Editor,” in Joby Milo Anthony and Howard Whitley Eves, In Eves’ Circles, 1994.)
|


