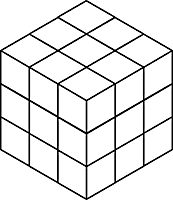
A mouse wants to eat his way through a 3 × 3 × 3 cube of cheese, starting in one of the corners and tunneling through all 27 1 × 1 × 1 sub-cubes, visiting each once. Can he arrange his route so that he finishes at the center of the cube? Assume that he always moves between orthogonally adjacent cubes, traveling through walls but not through edges or corners.
|
SelectClick for Answer |
No, it’s not possible. Imagine that the corner sub-cubes are black and that any two sub-cubes that share a face are of different colors:

Because the mouse always travels orthogonally, it will visit black and white squares alternately. And because the large cube contains an odd number of sub-cubes, any such route that starts in a black sub-cube and tours the whole cube must end in a black sub-cube. But the center sub-cube is white. So the task is impossible.
(From “Mathematical Mayhem,” Crux Mathematicorum 28:1 [February 2002], 34.)
|


