Line Limit - Futility Closet

Line Limit

You own a goat and a meadow. The meadow is in the shape of an equilateral triangle each side of which is 100 meters long. The goat is tied to a post at one corner of the meadow. How long should you make the tether in order to give the goat access to exactly half the meadow?

	Select Click for Answer
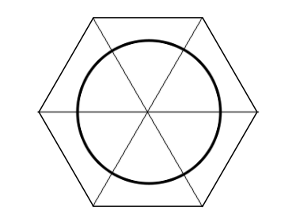
Draw a hexagon whose sides are 100 meters long. Now draw a circle, with the same center, whose radius r is the desired length of the tether: The difference in area between the hexagon and the circle is 6 times half the area of the meadow. The area of the circle is πr². The area of an equilateral triangle with side length a is $\displaystyle \frac{a^{2}\sqrt{3}}{4}$ . The area of a hexagon with side length a is $\displaystyle \frac{6a^{2}\sqrt{3}}{4}$ . For a = 100 the area of the hexagon is 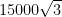$\displaystyle 15000\sqrt{3}$ . 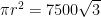If we want a circle half that size, then $\displaystyle \pi r^{2} = 7500\sqrt{3}$ and $\displaystyle r = \sqrt{\frac{7500\sqrt{3}}{\pi }} \approx 64.3037.$ (From Ian Stewart’s Cabinet of Mathematical Curiosities, 2009.)

Click for Answer

September 23, 2018September 24, 2018 | Puzzles