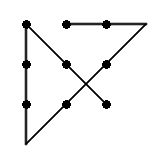
An old puzzle asks: Without lifting your pencil from the paper, can you draw a series of four straight lines that passes through all nine points in this grid?

The trick is to realize that the lines can extend beyond the grid’s area:
In 1970 Solomon Golomb and John Selfridge found a way to draw a closed path of eight segments that passes through all 25 points in this grid:

Can you?
|
SelectClick for Answer |
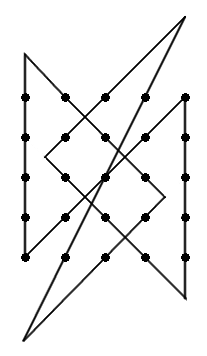
“This remarkable construction contains a line of slope 2, and has turning points for the path which not only are not lattice points, but do not lie on the grid lines (horizontal or vertical) through the lattice points.”
(Solomon W. Golomb and John L. Selfridge, “Unicursal Polygonal Paths and Other Graphs on Point Lattices,” Pi Mu Epsilon Journal 5:3 [Fall 1970], 107-117.)
|




