You’re holding a penny, and you’re standing on an infinite plane. The plane bears a grid of squares, each of which is twice the width of the penny. If you roll the penny out onto the grid, what is the probability that it will come to rest entirely within a square? (Assume the lines are of negligible thickness.)
|
SelectClick for Answer |
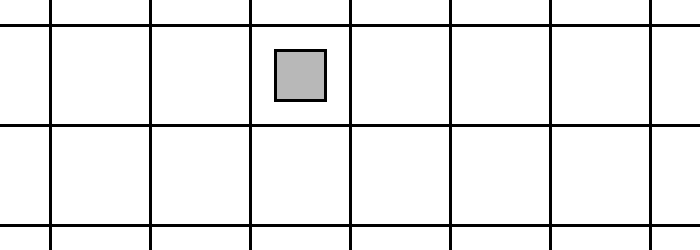
If the penny is to lie entirely within a square, then its center must fall within a square region one radius from the square’s edge. That region is the width of a penny, or one-fourth the square’s total area. So the probability is 1/4.
(From Ann Hirst, “Roll-a-Penny Probabilities,” Mathematical Gazette 73:464 [June 1989], 101-106.)
|


