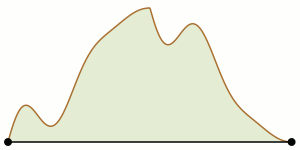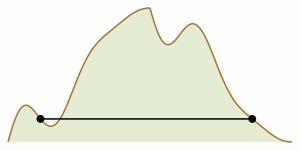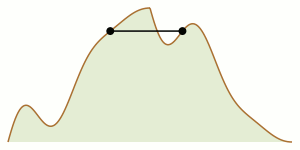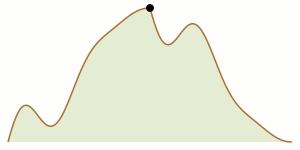
Two climbers stand on opposite sides of a two-dimensional mountain range. Is it always possible for both of them to make their way through the mountains, remaining constantly at the same altitude as one another, and arrive together at the top of the tallest peak?

The example shown here looks relatively straightforward, but that doesn’t prove that it’s possible in every mountain range. Each time either climber reaches a peak or a valley, she must decide whether to go forward or back, and in a complex range it’s not always clear whether there’s a series of choices that will lead both climbers to the goal.

As it turns out, though, the answer is yes. Alan Tucker gave an accessible explanation, using graph theory, in the November 1995 issue of Math Horizons.