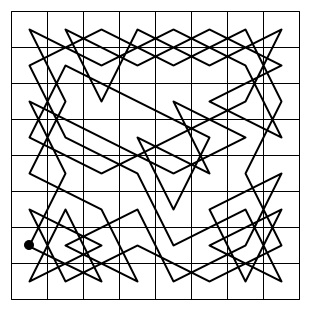
On a regular 8 × 8 chessboard, a wandering knight can visit each square once and then return to his starting square. Show that he can’t do this on an m × n board if m and n are both odd.
Home Again
An idler's miscellany of compendious amusements
On a regular 8 × 8 chessboard, a wandering knight can visit each square once and then return to his starting square. Show that he can’t do this on an m × n board if m and n are both odd.