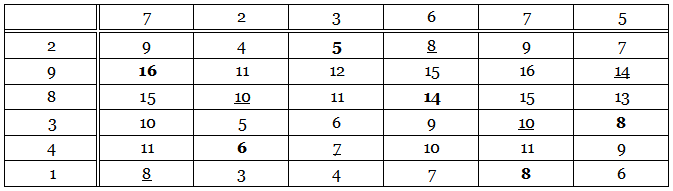
Each of the 36 numbers in this table is the sum of the numbers at the head of its column and at the left of its row. For example, 3 = 2 + 1 and 13 = 5 + 8. The six bold numbers have been chosen so that each of them falls in a different row and a different column. The underlined numbers were chosen in the same way. But each of these two sextets produces the same total: 16 + 6 + 5 + 14 + 8 + 8 = 8 + 10 + 7 + 8 + 10 + 14 = 57. In fact, any six numbers chosen in this way will produce the total 57. Why is this?